Тригонометрична таблиця – Повний гід для учнів і студентів

Тригонометрична таблиця — це важливий інструмент у математиці, який допомагає швидко знаходити значення тригонометричних функцій. Вона особливо корисна під час навчання у школі, коледжі або університеті. У цьому блозі ми детально розглянемо, що таке тригонометрична таблиця, як нею користуватись та чому вона так необхідна.

Що таке тригонометрична таблиця?

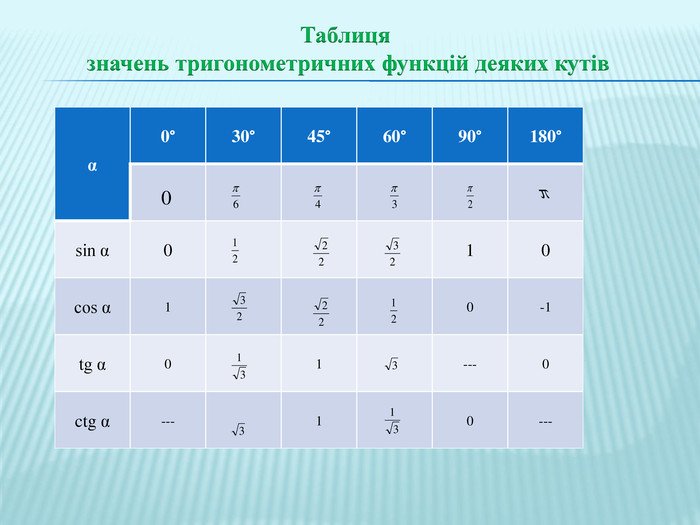
Тригонометрична таблиця — це таблиця, у якій зазначені значення тригонометричних функцій (синус, косинус, тангенс, котангенс) для деяких стандартних кутів. Наприклад, 0°, 30°, 45°, 60° і 90°. Вона дозволяє не рахувати вручну, а просто подивитись значення.

Навіщо потрібна тригонометрична таблиця?

Перш за все, тригонометрична таблиця дозволяє значно швидше виконувати математичні розрахунки. Завдяки цьому ви можете заощадити час на контрольній чи екзамені. Крім того, вона допомагає краще запам’ятати значення функцій.

Стандартні кути в тригонометричній таблиці

Тригонометрична таблиця зазвичай містить кути 0°, 30°, 45°, 60°, 90°. Для цих кутів можна легко запам’ятати основні значення:

Кут	sin	cos	tan	cot
0°	0	1	0	∞
30°	1/2	√3/2	√3/3	√3
45°	√2/2	√2/2	1	1
60°	√3/2	1/2	√3	√3/3
90°	1	0	∞	0

Як швидко запам’ятати тригонометричну таблицю?

Щоб легко запам’ятати значення, можна використовувати метод “пальців” або вивчити шаблони. Наприклад, значення sin для кутів можна записати як √0/2, √1/2, √2/2, √3/2, √4/2 відповідно для 0°, 30°, 45°, 60°, 90°. Це дуже зручно!

Застосування тригонометричної таблиці у навчанні

Тригонометрична таблиця часто використовується у задачах з геометрії, алгебри та фізики. Якщо потрібно знайти довжину сторони трикутника або кут, таблиця стане в нагоді. Навіть у ЗНО або НМТ вона часто виручає.

Як використовувати тригонометричну таблицю на практиці?

Під час розв’язування задач ви просто шукаєте потрібний кут і функцію, потім дивитеся значення. Наприклад, якщо треба знайти sin(30°), ви відкриваєте таблицю й бачите, що це 1/2. Далі підставляєте це в формулу.

Формули та зв’язок з таблицею

Формули тригонометрії, наприклад sin²(α) + cos²(α) = 1, дуже тісно пов’язані з таблицею. Знаючи значення з таблиці, легко перевірити, чи правильно ви підставили числа. Це дуже зручно.

Розв’язання прикладів з використанням таблиці

Приклад 1:
Знайти значення виразу: cos(60°) + sin(30°)
Розв’язання:
cos(60°) = 1/2, sin(30°) = 1/2
Отже, відповідь: 1

Приклад 2:
Обчислити tan(45°) × cot(45°)
tan(45°) = 1, cot(45°) = 1
Відповідь: 1

Чому важливо розуміти таблицю, а не просто вчити напам’ять?

Запам’ятати — добре, але розуміння дозволяє застосовувати знання у будь-якій ситуації. Якщо ви зрозуміли, чому sin(0°) = 0, а cos(0°) = 1, ви зможете використовувати ці знання не тільки на уроці, а й у реальному житті — наприклад, у будівництві або кресленні.

Як використовують тригонометричну таблицю у вищій математиці?

У вищій математиці таблиця — це лише старт. Далі ви будете працювати з будь-якими кутами, навіть нецілими, як-от 37° або 82°. Але база з таблиці допомагає побудувати логіку мислення.

Чи потрібна тригонометрична таблиця в епоху калькуляторів?

Так, безумовно! Хоч калькулятори й обчислюють значення автоматично, на ЗНО або в класі не завжди дозволяють їх використовувати. А ще таблиця тренує пам’ять, що корисно у будь-якому віці.

Поради щодо вивчення тригонометричної таблиці

1. Вивчайте по кутах — один кут на день.
   
2. Робіть маленькі шпаргалки.
   
3. Пояснюйте друзям — це зміцнює знання.
   
4. Практикуйтесь на прикладах.
   
5. Використовуйте кольорові позначки або стікери.
   

Мнемонічні правила

Запам’ятати “sin → √0,1,2,3,4 /2” і “cos → √4,3,2,1,0 /2” — це класичне мнемонічне правило. Воно допомагає вивчити таблицю за кілька хвилин.

Використання в шкільній програмі

Тригонометрична таблиця включається в програму 9–11 класів. Вона потрібна для розв’язання рівнянь, побудови графіків і підготовки до ЗНО. З нею учні можуть швидше та впевненіше вирішувати завдання.

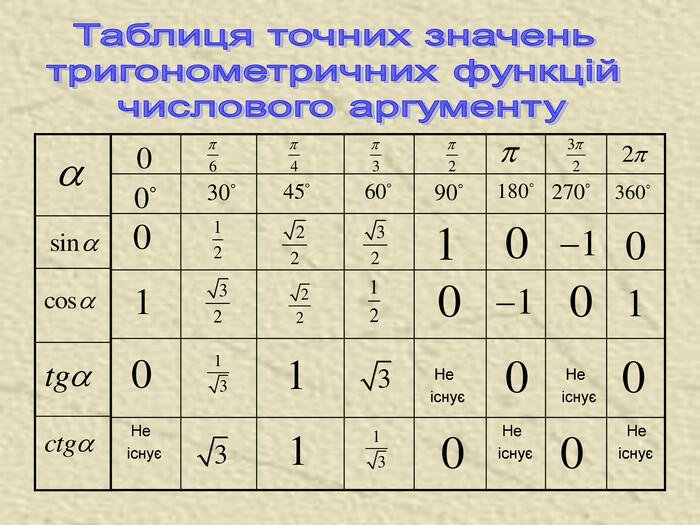
Чи існує тригонометрична таблиця для радіан?

Так, вона також є. Наприклад:
0 рад = 0°, π/6 рад = 30°, π/4 рад = 45°, π/3 рад = 60°, π/2 рад = 90°.
Це зручно для вивчення вищої математики.

Онлайн-ресурси з тригонометричною таблицею

Є багато сайтів, де можна знайти таблицю:

• Wikipedia
  
• Mathisfun
  
• Symbolab
  
• GeoGebra
  

Також існують мобільні додатки, де таблиця доступна у зручному вигляді.

Часті помилки при використанні таблиці

1. Плутання синуса і косинуса.
   
2. Підстановка неправильного кута.
   
3. Використання градусів замість радіанів.
   
4. Неправильне округлення дробів.
   

Уникаючи цих помилок, ви зможете точно розв’язувати задачі.

Висновок

Тригонометрична таблиця — це незамінний інструмент для кожного учня. Вона економить час, підвищує точність і допомагає краще розуміти тригонометрію. Використовуйте її щодня, і ви побачите результати вже за кілька тижнів.

Читати далі: Прийменник це – Повний гід для учнів та батьків

Часті запитання про тригонометричну таблицю