Що таке ірраціональні числа – повний гід для школярів

Ірраціональні числа — це числа, які не можна записати у вигляді звичайного дробу. Вони не мають точного десяткового значення, що повторюється або закінчується. У цій статті ми пояснимо, що таке ірраціональні числа, чим вони відрізняються від раціональних, де вони використовуються та чому вони такі важливі в математиці.

Що таке ірраціональні числа

Ірраціональні числа — це такі числа, які не можна представити як відношення двох цілих чисел. Наприклад, число √2 не можна точно записати у вигляді дробу, тому що його десяткове представлення нескінченне й не має періоду: 1.4142135…

Основна різниця між раціональними й ірраціональними числами

По-перше, раціональні числа мають точний запис. Це можуть бути прості дроби, як 1/2 або 3/4, або десяткові числа з кінцем, як 0.75. По-друге, ірраціональні числа ніколи не мають повторюваної частини. Наприклад, число π (пі) дорівнює приблизно 3.14159265…, але ця послідовність ніколи не зупиняється й не повторюється.

Приклади ірраціональних чисел

Деякі найвідоміші ірраціональні числа:

• √2 – корінь з двох
  
• π – відношення довжини кола до діаметра
  
• e – основа натурального логарифму
  
• Золотий перетин (φ) – приблизно 1.618033…
  

Ці числа не просто цікаві — вони зустрічаються в природі, архітектурі та науці.

Історія відкриття ірраціональних чисел

Ще в Давній Греції піфагорійці були впевнені, що всі числа можуть бути раціональними. Але коли було відкрито, що корінь з двох неможливо подати як дріб, це спричинило справжній шок. Згідно з легендою, Гіппас, який це довів, був вигнаний з математичної спільноти. Хоч це звучить драматично, але цей момент став ключовим у розвитку математики.

Як розпізнати ірраціональне число

Іноді буває складно відразу визначити, чи є число ірраціональним. Але є кілька підказок:

• Якщо корінь із числа не дає цілого результату (наприклад, √5), це зазвичай ірраціональне число.
  
• Якщо десятковий запис нескінченний і не має повторюваного шаблону — це також ознака ірраціонального числа.
  
• Якщо ви не можете записати число у вигляді дробу — це точно ірраціональне число.
  

Ірраціональні числаа в реальному житті

Можливо, ви думаєте: “А навіщо мені ці ірраціональні числаа?” Насправді вони часто з’являються в інженерії, дизайні, будівництві, фізиці. Наприклад:

• При розрахунках площ кола використовується число π.
  
• При моделюванні росту населення застосовується число e.
  
• У дизайні архітектурних об’єктів зустрічається золотий перетин φ.
  

Роль ірраціональних чисел у математиці

Ірраціональні числаа не лише доповнюють наше розуміння числової прямої, а й дозволяють нам розв’язувати складні рівняння. Без них алгебра, геометрія та математичний аналіз були б дуже обмеженими. Наприклад, рівняння x² = 2 не має раціонального розв’язку, але має ірраціональний – √2.

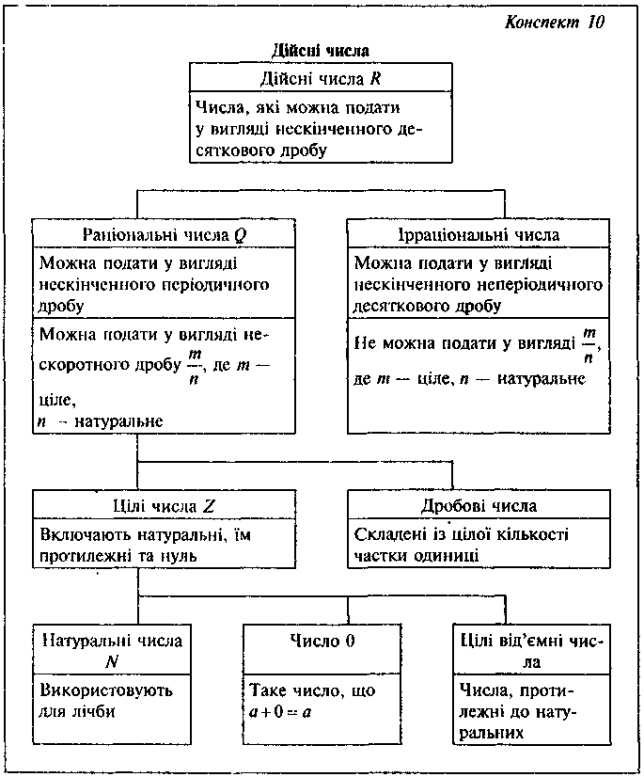
Порівняння: ірраціональні, раціональні й дійсні числаа

Усі ірраціональні числаа входять до множини дійсних чисел. Водночас, дійсні числа складаються з раціональних і ірраціональних. Це означає, що пряма чисел повна: кожна точка на прямій відповідає дійсному числу — або раціональному, або ірраціональному.

Як обчислювати з ірраціональними числами

Хоча ці числа не можна точно записати, з ними можна виконувати всі стандартні математичні операції: додавання, множення, віднімання тощо. Наприклад:

• π + 2 = приблизно 5.1416
  
• √2 × √3 = √6 ≈ 2.449
  

Тільки потрібно пам’ятати, що результат часто теж буде ірраціональним.

Чому важливо розуміти ірраціональні числаа в школі

Ірраціональні числаа входять до навчальної програми математики вже з середньої школи. Їхнє розуміння допомагає:

• краще орієнтуватися в складніших розділах, як алгебра й тригонометрія
  
• готуватися до ЗНО та олімпіад
  
• розвивати логічне мислення
  

Цікаві факти про ірраціональні числаа

1. У 2005 році було обчислено понад 1 трильйон знаків числа π.
   
2. e використовується в банківських формулах для розрахунку складних відсотків.
   
3. Золотий перетин зустрічається в мистецтві, наприклад, у картинах Леонардо да Вінчі.
   

Чи можна уявити ірраціональне число в геометрії?

Так! Наприклад, якщо побудувати квадрат зі стороною 1 см, то діагональ цього квадрата дорівнюватиме √2 см. І ось ви вже бачите ірраціональне число в реальному житті. Тому геометрія часто допомагає зрозуміти абстрактні поняття.

Чи можуть ірраціональні числа бути негативними?

Звичайно. Наприклад, –√3 — це ірраціональне число. Якщо додатне число ірраціональне, то й його від’ємник також буде ірраціональним.

Висновок

Ірраціональні числа — це надзвичайно важлива частина математики. Вони допомагають нам розуміти світ, будувати точні моделі, і розв’язувати задачі, які не під силу простим дробам. Знати, що таке ірраціональні числа, означає мати ще один ключ до розуміння нашого Всесвіту.

Читати далі: Тригонометрична таблиця – Повний гід для учнів і студентів

Часті запитання про ірраціональні числа